일상생활이나 공무원?시험, 감정평가사, 공인중개사, 자격증 시험 준비를 위해 계산기를 사용할 때가 있다. 휴대폰에도 계산기 기능이 있는데, 계산방식이 보통이지? 없어서 잘못 쓰면 엉뚱한 값이 뛴다. 물론 시험장에선 휴대전화나 공학용 재무용 계산기를 쓸 수 없다. 그래서 계산기를 사용해서 잘 알고 싶은 숫자를 쉽고 올바르게 구하는 방법을 핵심적인 것만 적어 보았다.
컴퓨터매뉴얼 : 카시오 AX-120ST 알고보면 편리한 컴퓨터 사용법, 공무원시험(아마), 공인중개사, 감정평가사, 일반사무원필독템…..
계산기는 버튼을 누르면 본체가 떠서 딱딱 소리가 나기 때문에 다른 쿠션을 만들어서 소리가 나지 않고 움직이지 않도록 하고 있습니다.
[ ]는 누르는 것이 아니다.
[step 1] 간단한 사칙연산과 계산기 버튼 사용법
사례 0) 삭제가 쉽지만 모르면 당황하는 기능 메모리된 숫자까지 모두 삭제하는 [GT GT MC AC]를 순차적으로 누른다
메모리가 없을 때(또는 메모리는 지우지 않고 나머지만 모두 지울 때)는 [GT GT AC]
0.1을 누르려면 [1]을 누르면 0.1이 된다.
몇 퍼센트를 손에 넣을 때, 예를 들어 10 퍼센트는 [0.1]을 눌러도 되고 [10 퍼센트]를 눌러도 된다. 예를 들어 200의 10%를 구하려면 [200 X 10%]를 누르면 된다.
사례1) 마진율을 요구하는 120만원의 상품을 취하고, 25%마진을 얻으려면 얼마에 팔아야 하는가.[120÷25 MU] 를 차례로 누른다 =160160만원에 팔아야
그럼 마진은 얼마인지 [MU]를 누른다 = 40만원 では
이 사례는 쇼핑몰 수수료가 25프로라면 내가 120만원을 받기 위해 판매가격이 얼마는 돼야 하는지와 같다.사실 [120÷.75 ] 과 같은 값 돌려주기 ㅋㅋ
사례 2) 전체에서 100이 되기 위한 비율 80에 몇 프로를 더하면 100이 되는가? 100 = 80 + ?%
[100 – 80 MU] 를 차례로 누른다 = 25 { “80에 80의 25%를 더하면 100이 된다”는 의미 }
사례 3) 총계 5 X 6 = 302 X 8
[GT GTAC 5 X 6 = ] [2 X 8 = ] [GT ] 를 순차적으로 누른다 = 46
사례 4) 가중평균 이익율 10%의 확률 30% = 3 이익률 20%의 확률 40% = 8 이익율 30%의 확률 30% = 9 ā 위의 세 가지 상황별 가중평균 수익률은 20%이다.
[GT GTAC 10 X.3 = ] [20 X.4 = ] [30 X.3 = ] [GT ] 를 차례차례 누른다 = 20
사례5) 현재 현금의 미래가치를 찾는 연간 이자율 10%인 경우 현재의 1원은 5년 후 얼마가 되는가?
[ GT GTMC AC 1.1 X 1.1 ==== ] = 1.61051 우리는 이것을 “현금박치기”라고 하고 즉, 방금 받은 “현금의 미래 가치”라고 한다.좀 고상한 말로 “일시불인 내가 훈계”라고 한다.
사례6) 판돈의 현재 가치를 구한다. 흔히 말하는 배짱이다. 연간 이자율 10%일 때 5년 후에 받는 1원은 현재 얼마 정도야?
[ GT GTMC AC 1.1 X 1.1 = M+1÷ MR = ] = 0.620921 우리는 이것을 “얼마면 빈 깡통 해주겠다” “(위험에 대한 보상도 더 있지만) 어음담보 균열이다. 이런 것을 지금 외상으로 팔아 (나중에) 받는 돈의 현재가치라고 한다.조금 고상한 말로 “일시불의 현가 계수”라고 한다.
여기서 알 수 있는 것은 [1÷1.61051 (일시불의 내가 계수)] =”일시불의 현가 계수”라고 하는 것이다.그럼, 당연 [1÷일시불의 현가 계수]=”일시불의 현가 계수”가 된다.
즉, 일시불의 현가계수는 일시불의 내가계수의 역수다.숫자놀이를 말로 하면 「일괄지불의 현가계수×일괄지불의 내가계수」=1이 된다.
여기서, 시사하는 바는 역수는 분자 분모를 뒤엎은 것이다. 초등학교 차원의 진리인데도, 실제로 실생활에서 쓰려고 하면 생각나지 않는다. 그러면 초등학생 수준에서 풀어보자.
이렇게 보면 쉽지만 막상 시험이나 실생활에 직면하면 당황해요. 알아두면 아주 요긴하게 사용할 거예요.
이쯤에서만 연금의 현가계수, 저당상 연금의 내가계수, 감채기금수를 눈 깜짝할 사이에 구할 수 있다.이것이 재무의 첫걸음이다.보통 이러한 계수와 정수는 연간 단위로 하되, 연말에 넣었다 빼는 것을 기준으로 한다.말은 너무 어려워. 이렇게 이해하면 검과 쉽다.
연금의 현가계수:나중에 늙어 매년 받는 돈을 자녀들에게 결혼시키기 위해 당장 찾으면 얼마나 되느냐는 것이다.유식하게 이렇게 말하는 매년 1원씩 n년간 받게 되는 연금을 일시불로 환원해 준 금액(을 요구).
저당수:1억 빌리면 매년 얼마씩 갚아야 하는지: 유식하게 이렇게 말하는 1원을 n년 만기에 원리금균등상환 방식으로 대출받았을 때 매년 말에 상황을 개선해야 할 원리금을 찾는다.연금의 현가 계수의 역수
연금 내가 계수: 매년 꼬박꼬박 저금하면(10년) 얼마 받나? 유식하게 이렇게 말하는 매년 1원씩 받게 될 연금을 (매년 1원씩) 적립할 경우 n년 후에 받게 될 금액(을 구함)
감채기금계수: 목표달성 위해선 얼마씩 투입해야 할까? 10년 안에 강남에 아파트 한 채 살려면 매년 얼마씩 넣어야 하나?) : 유식하게 이렇게 말한다. n년 후에 1원을 만들기 위해 매 기간마다 적립해야 하는 금액(을 요구).연금의 내가 계수의 역수
주의 : 보통 이자율 r을 생략해서 표현하는데 이자율 r이 몇 %인 경우 가 생략되었다고 보면 된다.기말 기준
[step 2] 연금의 현가계수와 저당상수
잘 잤어요?이제는 고급 단계로 곽국신
2. 1년금의 현가이며, 그러면 연금의 현가계수를 연금의 현가계수를 이용하여 찾아봅시다. 일단 연금의 현가계수는 아래와 같은데 딱 보면 대박이죠?
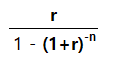
그런데 말입니다.이걸 열어보면 굉장히 간단합니다. (1+r) 모든 식의 핵심입니다먼저 (1+r)n이 바로 위에서 요구한 일시불의 현가입니다.이해를 용이하게 하기 위해 위와 같은 사례에서 이자율 10%로 5년을 가정하면 이 값은 0.620921입니다. 요구하는 원리는 위의 내용을 참고하시기 바랍니다. 결과적으로 아래와 같이 구하면 됩니다.
[ 1 . 1 X 1 . 1 = = = = M + 1 ÷ MR = ]
지금 [MCM+] 를 클릭하면 0.620921 (이 생략) 가 기존 메모리를 삭제하고 새로 저장됩니다.
연금의 현가계수를 찾아봅시다.
[1 – MR ÷.1 = ] 됐습니다
그러면 3.790787이 나와요 빙고 이게 연금의 현재 가치예요3.790787 이게 매년 말 1원씩 5년간 받는 돈의 현재 가치입니다.다르게 말하면 이자가 10%일 때 매년 말에 1백만원씩 5년간 받을 금액을 일시불로 받으면 379만787원을 받게 된다는 것입니다. 물론 이자율이 좋을 때 얘기죠. 이자가 내리면 받는 돈은 더 높아지겠죠. 즉, 분모인 r(0.1)이 r(0.03)로 바뀌면 빈자리가 적어지므로 일시불로 받는 돈은 커집니다.
돌려드릴 돈도 같은 방법으로 계산을 하시면 됩니다.
2.2 저당 상수로 그러면 저당 상수를 찾아볼게요저당정수는 연금의 현가계수 역수이므로 앞으로는 요놈을 뒤집어 계산하면 원리금균등상환방식으로 대출 시 매년 상환해야 하는 원리금을 얻을 수 있습니다.
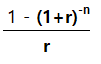
자, 뒤집겠습니다

약간 ‘아레’네요
이렇게 됩니다.
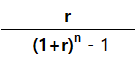
그런데 우리는 이미 연금의 현가계수를 구했으므로
[ 1 ÷ 3.790797 = ]
하면 바로 저당상수(0.263797)가 됩니다.
재밌다!
연금의 내가 계수는 아이고 얘는 언제 하는지…
[step 3] 연금의 자기계수와 감채기금계수
3.1년금의 자기계수(매년 일정액씩) 적립
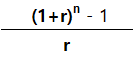
3.2 감채기금계수 감채기금계수는 연금의 자기계수와 역수관계
일정 목표금액을 달성하기 위해 매년 저축하는 금액

[step4] 핵심 정리 항목의 핵심 내용 비고 KFS(1+r) 모두는(1+r)로 구성된다.시가계수 -n승 미래의 가치를 현재의 가치로 싸게 보는 것(할인)은 -n승이다 내가 계수 n승 현재의 돈을 미래가치로 예상하는 것은 오직 n승이다
r ↑가 커지면 현재가치 ↑ 밀리가치 ↑ 연금의 현가계수 ↑ 연금의 현가계수 ↑ 저당정수 ↑ 감채기금계수 ↓